A gallery of randomly generated art

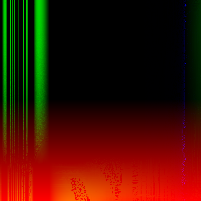
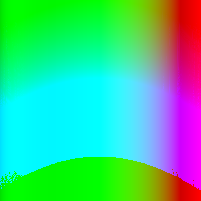
In a paper from CMU, security researchers describe a nifty algorithm used to generate random images known as RandomArt. In a nutshell, the algorithm takes as input a seed to a pseudo-random number generator and uses it to construct an abstract syntax tree by selecting rules from a predefined grammar. The AST describes a function mapping (x, y) pixel values to RGB values.

Recently I implemented a version of it in Haskell, and this page shows some images I was able to generate using a pretty simple grammar. Each image uses a different initial seed, so you can see that altering the seed results in a wildly different image, making it suitable for quickly spotting changes in, for instance, SSH public keys.

See the appendix for more details about how this works and how to generate your own images.

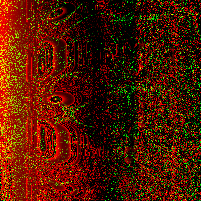
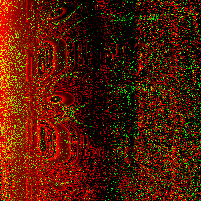
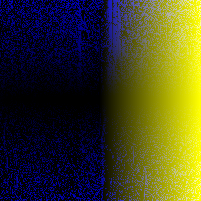
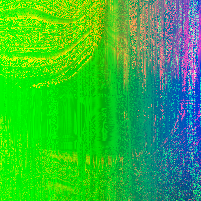
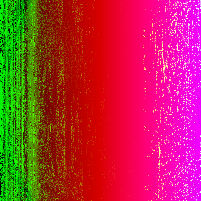
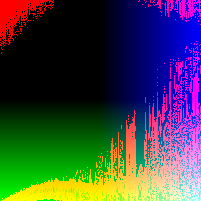
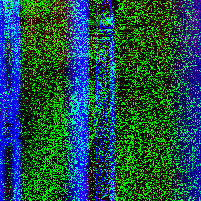
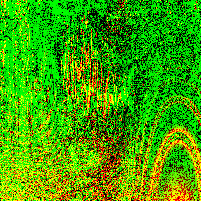
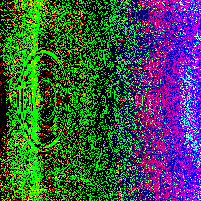
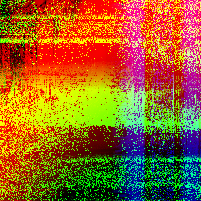
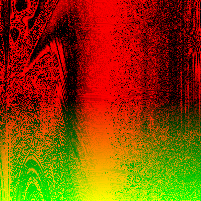
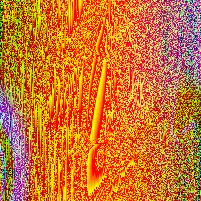
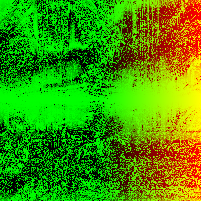
Appendix

Usage

You can generate an image by cloning the randomart program and running it:

git clone https://github.com/jamesma100/randomart && cd randomart
cabal run -- randomart [--d <depth>] [--p <pixels>] [-o <filepath>] [-s <seed>]

For example:

cabal run -- randomart --d 25 --p 200 -o ./my_img.png -s my_happy_seed

The above images were generated in a loop with a different seed each time:

for i in {1..60}; do cabal run randomart -- -p 200 -o ./images/${i}.png -d 35 \
-s $(echo $RANDOM | shasum -a 256 | awk '{print $1}' /dev/stdin); done

Details

The grammar I used looks like:

ruleA = RuleNode [RandNode, RandNode, XNode, YNode]
ruleC = RuleNode
  [ruleA
  ,ruleA
  ,SinNode (AddNode ruleC ruleC)
  ,CosNode (AddNode ruleC ruleC)
  ,TanNode (AddNode ruleC ruleC)
  ,SinNode (MultNode ruleC ruleC)
  ,CosNode (MultNode ruleC ruleC)
  ,TanNode (MultNode ruleC ruleC)
 ]
ruleE = RuleNode [TripleNode ruleC ruleC ruleC]
grammar = [ruleA, ruleC, ruleE] :: Grammar

You can create your own grammar by composing different rules, and that’ll change how your AST is constructed, and hence how your image is generated. Rules can be anything from trigonometric functions to if-else statements. I defined these as different constructors for the same data type.

data Node =
  NumberNode Double |
  BoolNode Bool |
  RandNode |
  SinNode Node |
  CosNode Node |
  TanNode Node |
  XNode |
  YNode |
  AddNode Node Node |
  MultNode Node Node |
  ModNode Node Node |
  ExpNode Double Node |
  TripleNode Node Node Node |
  GTNode Node Node |
  GTENode Node Node |
  LTNode Node Node |
  LTENode Node Node |
  IfNode Node Node Node |
  NormNode Node |
  NullNode |
  RuleNode [Node]
  deriving Show

Hints

It’s hard to predict what your generated image will look like, but in general a larger depth and a non-linear ruleset will give you more detailed images. However, sometimes your image will still be very simple if a terminal node is selected early on and the algorithm halts. Note that the first rule of your grammar (e.g. ruleA above) must be terminal, otherwise the algorithm will not halt.

For more details, you should read the paper.